The cost of being Greedy

When trying to teach robots or machines to perform tasks, we devise algorithms for them to follow. Some algorithms are good, some are bad. Some take a long time to finish, others never finish at all. Algorithms are judged in comparison to some optimal algorithm. Oftentimes this optimal algorithm is only theoretical - we can never implement it, but we know how it would perform if we could. 

Getting to optimal yields marginally diminishing returns - think about walking on an incline, where every step you take means a 1% increase in the slope. It gets harder and harder to keep increasing. Eventually you get high enough, even though you don't get to the top.

In this sense, we can think about Greedy algorithms. Greedy is a very simple heuristic for getting partially up the incline. And using some maths, we are guaranteed to always get a pretty good way up - but rarely will we ever get to the top. The key point being that implementing a Greedy Algorithm is usually VERY easy. Let's see an example:

Imagine trying to solve the following problem:

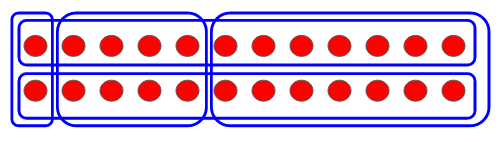
What is the minimum number of covers (blue outlines) required to cover all of the red dots in the figure below.

Easy right? Just use the two long covers. 

But how do we teach a robot to perform this task? It might seem trivial, but solving this problem in general is actually NP-Hard. Real world examples of these types of problems are:

• Where to place cameras in a house such that the entire house is covered with the minimum number of cameras
• How to minimize number of cell towers to cover the most number of people in a city
• Which podcasts to advertise on such that each of your users hears the ad while minimizing overlap among podcasts (because each ad costs your company money)

Figuring out how many cameras/towers/podcasts and where to place them/which to purchase is hard to do perfectly. So instead of solving it exactly, let's implement a Greedy algorithm.

In computer science speak, Greedy just means that our algorithm will pick the best possible next choice, given a number of different options. Humans are greedy in this sense all the time - for example: Scheduling your classes in school. You can greedily pick your favorite course first, then your second favorite, and so on. However, what if your favorite course overlaps with your second and third favorites, and the next available course is your 4th favorite? Is it better to be enrolled in your 1st and 4th choices or your 2nd and 3rd? It's not obvious to me. Clearly being greedy is suboptimal, but perhaps its not a bad default.

So how does Greedy work in Set Cover problem? It will choose the set that covers the most uncovered dots at every step, until it covers some proportion (up to you how much) of the dots. In our example, the following 3 covers will be chosen:

Clearly not optimal (because 3 covers is worse than 2 covers), but simple enough to teach a robot!